Srinivasa Ramanujan FRS (1887 – 1920) was a self-taught Indian mathematical genius who made numerous contributions in several mathematical fields including mathematical analysis, infinite series, continued fractions, number theory and game theory. Ramanujan provided solutions to mathematical problems that were then considered unsolvable. Moreover, some of his work was so ahead of his time that mathematicians are still understanding its relevance. In 1914, Ramanujan found a formula for computing π (pi) that is currently the basis for the fastest algorithms used to calculate π. The circle method, which he developed with G. H. Hardy, constitute a large area of current mathematical research. Moreover, Ramanujan discovered K3 surfaces which play key roles today in string theory and quantum physics; while his mock modular forms are being used in an effort to unlock the secret of black holes. Know more about the achievements of Srinivasa Ramanujan through his 10 major contributions to mathematics.
#1 HE WAS THE SECOND INDIAN TO BE ELECTED A FELLOW OF THE ROYAL SOCIETY
A self-taught genius, Ramanujan moved to England in March 1914 after his talent was recognized by British mathematician G. H. Hardy. In 1916, Ramanujan was awarded a Bachelor of Science by Research degree (later named Ph.D.) by Cambridge even though he was not an undergraduate. The Ph.D. was awarded in recognition of his work on ‘Highly composite numbers’. In 1918, Ramanujan became one of the youngest Fellows of the Royal Society and only the second Indian member. The same year he was elected a Fellow of Trinity College, Cambridge, the first Indian to be so honored. During his short lifespan of 32 years, Ramanujan independently compiled around 3,900 results. Apart from the below mentioned achievements his contributions include developing the relationship between partial sums and hyper-geometric series; independently discovering Bernoulli numbers and using these numbers to formulated the value of Euler’s constant up to 15 decimal places; discovering the Ramanujan prime number and the Landau–Ramanujan constant; and coming up with Ramanujan’s sum and the Ramanujan’s master theorem.

#2 THE FASTEST ALGORITHMS FOR CALCULATION OF PI ARE BASED ON HIS SERIES
Finding an accurate approximation of π (pi) has been one of the most important challenges in the history of mathematics. In 1914, Srinivasa Ramanujan found a formula for computing pi that converges rapidly. His formula computes a further eight decimal places of π with each term in the series. It was in 1989, that Chudnovsky brothers computed π to over 1 billion decimal places on a supercomputer using a variation of Ramanujan’s infinite series of π. This was a world record for computing the most digits of pi. Moreover, the Ramanujan series is currently the basis for the fastest algorithms used to calculate π.

#3 RAMANUJAN CONJECTURE PLAYED A KEY ROLE IN THE FAMOUS LANGLANDS PROGRAM
In 1916, Ramanujan published his paper titled “On certain arithmetical functions”. In the paper, Ramanujan investigated the properties of Fourier coefficients of modular forms. Though the theory of modular forms was not even developed then, he came up with three fundamental conjectures that served as a guiding force for its development. His first two conjectures helped develop the Hecke theory, which was formulated 20 years after his paper, in 1936, by German mathematician Erich Hecke. However, it was his last conjecture, known as the Ramanujan conjecture, that created a sensation in in 20th century mathematics. It played a pivotal role in the Langlands program, which began in 1970 through the proposal of American-Canadian mathematician Robert Langlands. The Langlands program aims to relate representation theory and algebraic number theory, two seemingly different fields of mathematics. It is widely viewed as the single biggest project in modern mathematical research. “On certain arithmetical functions” by Ramanujan thus effectively changed the course of 20th century mathematics.

#4 HE DEVELOPED THE INFLUENTIAL CIRCLE METHOD IN PARTITION NUMBER THEORY
Apartition for a positive integer n is the number of ways the integer can be expressed as a sum of positive integers. For example p(4) = 5. That means 4 can be expressed as a sum of positive integers in 5 ways: 4, 3+1, 2+2, 2+1+1 and 1+1+1 +1. Ramanujan, along with G. H. Hardy, invented the circle method which gave the first approximations of the partition of numbers beyond 200. This method was largely responsible for major advances in the 20th century of notoriously difficult problems such as Waring’s conjecture and other additive questions. The circle method is now one of the central tools of analytic number theory. Moreover, circle method and its refinements constitute a large area of current mathematical research.
#5 HE DISCOVERED THE THREE RAMANUJAN’S CONGRUENCES
Related to the Partition Theory of Numbers, Ramanujan also came up with three remarkable congruences for the partition function p(n). They are p(5n+4) = 0(mod 5); p(7n+4) = 0(mod 7); p(11n+6) = 0(mod 11). For example, the first congruence means that if an integer is 4 more than a multiple of 5, then number of its partitions is a multiple of 5. The study of Ramanujan type congruence is a popular research topic of number theory. It was in 2011, that a conceptual explanation for Ramanujan’s congruences was finally discovered. Ramanujan’s work on partition theory has applications in a number of areas including particle physics (particularly quantum field theory) and probability.
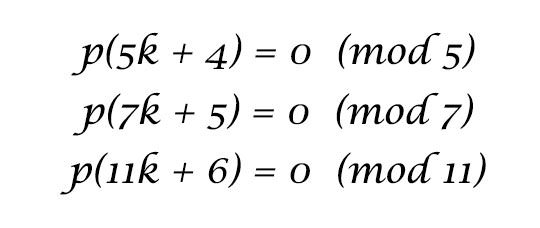
#6 NUMBER 1729 IS NAMED HARDY–RAMANUJAN NUMBER
In a famous incident British mathematician G. H. Hardy while visiting Ramanujan had ridden in a taxi cab with the number 1729. He remarked to Ramanujan that the number “seemed to me rather a dull one, and that I hoped it was not an unfavorable omen”. “No,” Ramanujan replied, “it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways.” The two different ways are: 1729 = 13 + 123 = 93 + 103. 1729 is now known as the Hardy–Ramanujan number. Moreover, numbers that are the smallest number that can be expressed as the sum of two cubes in n distinct ways are now referred to as taxicab numbers due to the incident. The relevance of 1729 has recently come to light as it was part of a much larger theory that Ramanujan was developing. Theorems have been established in theory of elliptic curves that involve this fascinating number.

#7 HE DID GROUNDBREAKING RESEARCH RELATED TO FERMAT’S LAST THEOREM
In 2013 famous Japanese American Mathematician Ken Ono, along with Sarah Trebat-Leder, found an equation by Ramanujan had clearly showed that he had been working on Fermat’s last theorem, one of the most notable and difficult to prove theorems in the history of mathematics. In 1637, French mathematician Pierre de Fermat had asserted that: if n is a whole number greater than 2, then there are no positive whole number triples x, y and z, such that xn + yn = zn. This means that there are no numbers which satisfy the equations: x3 + y3 = z3; x4 + y4 = z4; and so on. The equation of Ramanujan illustrates that he had found an infinite family of positive whole number triples x, y and z that very nearly, but not quite, satisfy Fermat’s equation for n=3. They are off only by plus or minus one. Among them is 1729, which misses the mark by 1 for x=9, y=10 and z=12. Moving forward, Ramanujan also considered the equations of the form: y2=x3+ ax + b. If you plot the points (x,y) for this equation you get an elliptic curve. Elliptic curves played a key role when English mathematician Sir Andrew Wiles finally proved Fermat’s last theorem in 1994, a feat described as a “stunning advance” in mathematics.
#8 RAMANUJAN WAS THE FIRST TO DISCOVER K3 SURFACES
Ken Ono also found that Ramanujan went on to discover an object more complicated than elliptic curves. When it was re-discovered in 1958 by Andre Weil, it was named K3 surface. Thus it has come to light that Ramanujan was using 1729 and elliptic curves to develop formulas for a K3 surface. “Elliptic curves and K3 surfaces form an important next frontier in mathematics and Ramanujan gave remarkable examples illustrating some of their features that we didn’t know before.” Moreover, K3 surfaces play key roles today in string theory and quantum physics. Like, string theory suggests that the world consists of more than the three dimensions that we can see. These extra dimensions are rolled up tightly in tiny little spaces too small for us to perceive. These tiny spaces have a particular geometric structure. Calabi–Yau manifold is a class of geometric objects that have similar structure and one of the simplest classes of Calabi-Yau manifolds comes from K3 surfaces.
#9 HIS THETA FUNCTION LIES AT THE HEART OF STRING THEORY IN PHYSICS
In mathematics, theta functions are special functions of several complex variables. German Mathematician Carl Gustav Jacob Jacobi came up with several closely related theta functions known as Jacobi theta functions. Theta functions were studied extensively by Ramanujan. He came up with the Ramanujan theta function, which generalizes the form of Jacobi theta functions while also capturing their general properties. In particular, the Jacobi triple product takes on an elegant form when written in terms of the Ramanujan theta function. Ramanujan theta function has several important applications. It is used to determine the critical dimensions in Bosonic string theory, superstring theory and M-theory.
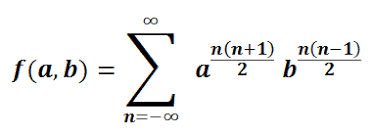
#10 HIS MOCK MODULAR FORMS MAY UNLOCK THE SECRET OF BLACK HOLES
In a 1920 letter to Hardy, Ramanujan described several new functions that behaved differently from known theta functions, or modular forms, and yet closely mimicked them. These were the first ever examples of mock modular forms. More than 80 years later, in 2002, a description for these functions was provided by Sander Zwegers. Further, Ramanujan predicted that his mock modular forms corresponded to ordinary modular forms producing similar outputs for roots of 1. Ken Ono ultimately showed that a mock modular form could be computed just as Ramanujan predicted. It was found as the output of mock modular forms shoot off to enormous numbers, the corresponding ordinary modular form expand at a similar rate and thus their difference is a relatively small number. Expansion of mock modular forms is now used to compute the entropy, or level of disorder, of black holes. Thus even through black holes were virtually unknown during his time, Ramanujan was able to do mathematics which may unlock their secret.


A major method for computation of Feynman integrals is the bracket integration method, a direct result from his Master Theorem (https://en.wikipedia.org/wiki/Ramanujan%27s_master_theorem)
What is plus and minus infinity, he used in his theta function? Infinity in two opposite directions?
very useful information but no that much recognition
awesome pic. loved it