Archimedes (c. 287 BC – c. 212 BC) was an ancient Greek mathematician, scientist and inventor who lived in the city of Syracuse in Sicily. He is considered one of the greatest mathematicians of all time and his contributions to the field include anticipating calculus; providing the first accurate estimation of the value of pi; and being the first to derive a formula for surface area and volume of a sphere. In physics, among other things, Archimedes formulated the famous Archimedes’ principle in the field of fluid mechanics; proved the law of the lever; and laid the foundation of hydrostatics with his work On Floating Bodies. Despite these contributions, during his time Archimedes was most known for inventing deadly war machines like the Claw of Archimedes. His other inventions include the Archimedes’ screw and the odometer. Know more about the numerous contributions of Archimedes through his 10 major achievements.
#1 HE FORMULATED THE ARCHIMEDES’ PRINCIPLE
One of the most famous contributions of Archimedes is the Archimedes’ principle. It is said to have been found by him when he was tasked to determine the purity of the gold crown of King Hiero II of Syracuse. The Archimedes’ principle states that a body totally or partially immersed in a fluid is subject to an upward force (buoyant force) that is equal in magnitude to the weight of fluid it displaces. Thus, the net upward force on the object is the difference between the buoyant force and its weight. If this net force is positive, the object rises; if negative, the object sinks; and if zero, the object remains in place without either rising or sinking. Archimedes’ principle is a law of physics fundamental to fluid mechanics and it has numerous applications including the hydrometer, which uses it to determine the specific gravity (relative density) of liquids; designing of ships and submarines; and in controlling the flight of a hot-air balloon.
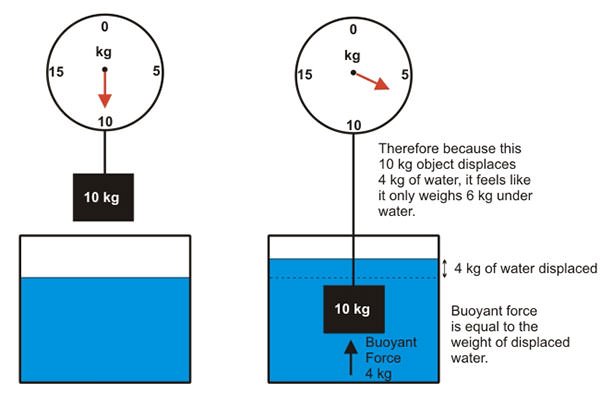
#2 HE WAS THE FIRST TO ESTABLISH THE LAW OF THE LEVER
A lever is a machine consisting of a rigid rod pivoted at a fixed hinge, or fulcrum. In his book On the Equilibrium of Planes, Archimedes proved the law of the lever using geometric reasoning. It shows that if the distance a from the fulcrum to where the input force is applied (point A) is greater than the distance b from fulcrum to where the output force is applied (point B), then the lever amplifies the input force. The reverse also holds true. Archimedes was also the first to introduce the concept of “center of mass”. In On the Equilibrium of Planes, he showed that the torque exerted on a lever by weights resting at various points along the lever is the same as what it would be if all of the weights were moved to a single point: their center of mass.
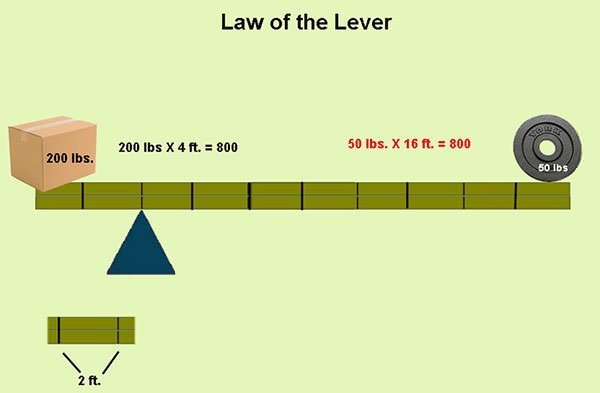
#3 He LAID THE FOUNDATION OF HYDROSTATICS
In his work On Floating Bodies, Archimedes established various general principles. These include the Archimedes’ principle; the Principle of flotation which states that any floating body displaces its own weight of fluid; and the prove that water will adopt a spherical form around a center of gravity. The book also contains a detailed investigation of the stable equilibrium positions of floating right paraboloids of various shapes and relative densities, when floating in a fluid of greater specific gravity, according to geometric and hydrostatic variations. On Floating Bodies is the first known work on hydrostatics and Archimedes is thus regarded as the founder of the discipline of hydrostatics.

#4 HE INVENTED AND USED METHODS SIMILAR TO CALCULUS
The method of exhaustion was a technique developed by ancient Greeks of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. As one increases the number of sides (n) of the polygon, the difference in area between the n-th polygon and the containing shape will become arbitrarily small. Archimedes made unprecedented use of the method of exhaustion to prove his mathematical discoveries. He also made the first known use of indivisibles. His method of indivisibles was similar to Cavalieri’s principle which works on the basis that if in two solids of equal altitude, the sections made by planes parallel to and at the same distance from their respective bases are always equal, then the volumes of the two solids are equal. The method of exhaustion and the method of indivisibles are regarded as forerunners to modern calculus.
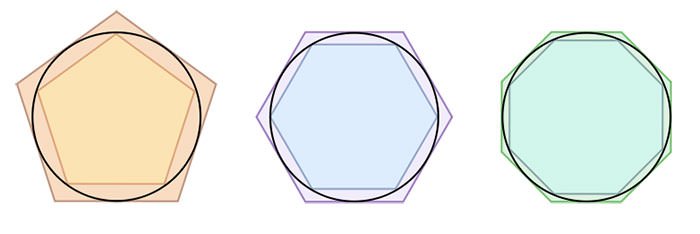
#5 HE IS CONSIDERED THE FIRST TO CALCULATE AN ACCURATE ESTIMATION OF PI
Pi (π) is one of the most important numbers in mathematics. The fact that the ratio of the circumference of a circle to its diameter was constant was known to many ancient cultures perhaps as early as 1900 BC and there values for the constant were close to 3.1. In his work Measurement of a Circle, Archimedes used the method of exhaustion to estimate the area of a circle. He drew a regular polygon outside a circle and a regular polygon inside it; and progressively increased the number of sides of both the polygons till they had 96 sides each. Apart from finding that the area of a circle was equal to π multiplied by the square of the radius of the circle (πr2), Archimedes determined that the value of π lay between 223/71 (approximately 3.1408) and 22/7 (approximately 3.1429). The exact value of pi cannot be found as it is an irrational number but his estimation was consistent with its approximate value of 3.1416. Archimedes’ upper bound has probably led to the widespread but incorrect belief that π is equal to 22/7. Archimedes is considered to be the first to calculate an accurate estimation of the value of pi and this is regarded as one of his greatest contributions.
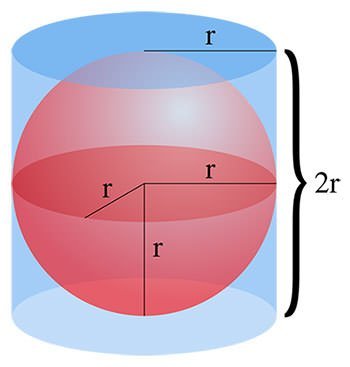
#6 HE DERIVEd A FORMULA FOR SURFACE AREA AND VOLUME OF A SPHERE
In his work, On the Sphere and Cylinder, Archimedes inscribed a sphere in a cylinder and used the method of indivisibles to become the first to derive a formula for the surface area (4πr2) and enclosed volume (4/3πr3) of a sphere. He then proved the results using the method of exhaustion. As the surface area of cylinder is 6πr2and its volume is 2πr3, Archimedes found that both the volume and the surface area of the sphere were two-thirds that of the cylinder of the same radius. Archimedes was most proud of this mathematical proof. In fact, he was so proud of this achievement that he requested a sculpted sphere and cylinder to be placed on his tomb.
#7 He WAS THE FIRST TO USE THE CONCEPT OF ACTUAL INFINITY
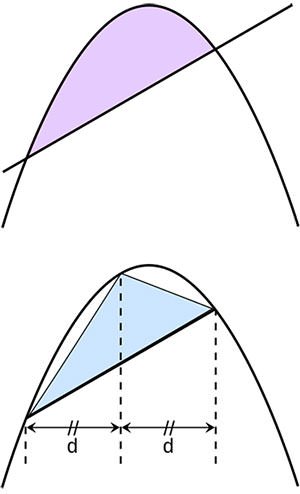
In his work The Quadrature of the Parabola, Archimedes used the method of exhaustion to prove that the area of a parabolic segment (the region enclosed by a parabola and a line) is 4/3 that of a certain inscribed triangle. This represents the most sophisticated use of the method of exhaustion in ancient mathematics, and remained unsurpassed until the development of integral calculus in the 17th century. Other contributions of Archimedes to mathematics include the first mathematical use of the concept of actual infinity, considered one of his major achievements; and his calculation of the value of the square root of 3 as lying between 265/153 (approximately 1.7320261) and 1351/780 (approximately 1.7320512), a very accurate estimate for the time as the actual value is approximately 1.7320508.
#8 He IS CREDITED WITH THE INVENTION OF ARCHIMEDES’ SCREW
Hiero II, King of Syracuse, commissioned Archimedes to design a huge ship. Known as Syracusia and built around 240 BC, it is claimed to be the largest transport vessel of antiquity. As the ship of such size would leak a considerable amount of water through the hull, Archimedes purportedly designed a machine in order to remove the bilge water. It became known as Archimedes’ screw and was most used to raise water for irrigation from a low lying body of water. The Archimedes screw consists of a helical screw inside a hollow tube. The whole thing is turned on its axis either by man or some other source of power. As it turns the bottom end, which is submerged in water, scoops up water inside the tube and releases it at the top end. Though archaeological evidence suggests that the machine was built before Archimedes in ancient Assyria, he is still credited with its invention. The Archimedes’ screw is still in use today for pumping liquids and granulated solids such as coal and grain.

#9 HE INVENTED AN INGENIOUS MACHINE CALLED CLAW OF ARCHIMEDES
Around 214 B.C., the Romans were attempting to siege Syracuse, a prominent Greek city. Archimedes was given the task of defending the seaside city and is said to have created a machine which is now famous as the Claw of Archimedes. It consisted of a hook system to lift and topple ships which approached the walls of the city. The Romans attacked Syracuse at night and the Claw machines sank many of their ships. According to legend they were so effective that the Romans didn’t know what hit them and wondered whether they were fighting against the Gods. The plausibility of the Claw of Archimedes was tested in a 1999 BBC series and its design was found to be workable.

#10 HE IS CREDITED WITH SEVERAL OTHER INVENTIONS
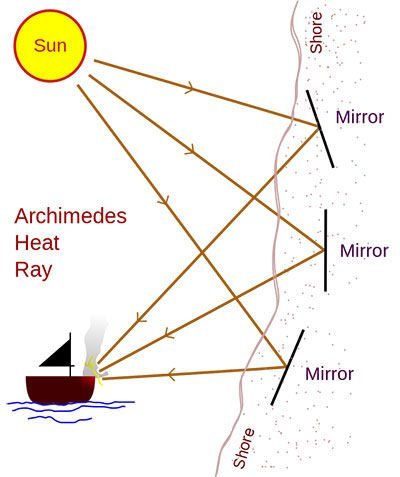
Archimedes is considered an ingenious inventor. Other inventions and discoveries credited to Archimedes include a block-and-tackle pulley system that allowed sailors to use the principle of leverage to lift objects that would otherwise have been too heavy to move; and the odometer, an instrument for measuring the distance traveled by a vehicle. Archimedes has also been credited with improving the power and accuracy of the catapult. A spectacular machine credited to Archimedes is the heat ray or the death ray. It is said to have used mirrors acting collectively as a parabolic reflector to burn ships attacking Syracuse. However most modern researchers consider such an invention as unlikely and a Massachusetts Institute of Technology team carried out an experiment that showed that such a machine wouldn’t be feasible at the time.
ARCHIMEDES AND ASTRONOMY
Archimedes was also an astronomer. Roman politician and lawyer Cicero, who lived several centuries after the death of Archimedes, wrote in one of his accounts that after the city of Syracuse was captured and destroyed by the Romans in 212 BC, they brought back a couple of devices which were allegedly built by Archimedes. One device mapped the sky on a sphere and the other predicted the motions of the sun, the moon and the planets. Previously this was considered unlikely. But the discovery of an ancient Greek device with similar capabilities, the Antikythera mechanism, has led many to believe that Archimedes did construct the alleged astronomical devices.


Maza aa gya
Aa ha!!
Dhanyawaad.
Very good
excellent work there